大家好,欢迎收看每天都进步,这里是天地海课室,陪你每天进步1%.
今天我们继续来聊π的故事。昨天我们说到了,为了寻找π这个圆周率的数值,很多的人为之做出了贡献,其中贡献最大的人,是阿基米德。阿基米德用内接外切正多边形的方法,来计算多边形的周长,无限逼近正确的答案。只要多边形的边长足够多,就可以计算出足够准确的π的数值。但是,在阿基米德被杀了之后,欧洲就有足足一千年的时间,没有在π的领域里面取得突破。
但是,欧洲这个地方没有突破,不代表其他地方没有突破。其中在亚洲就有三个地方对π的计算取得了重大的突破。首先第一个我们要聊的地方是中国。中国的刘徽以及祖冲之就对π的近似值计算取得了重大的突破。其中刘徽将π的近似值逼近到了3.1416,而祖冲之则把这个数字计算到了3.1415926到3.1415927之间。这成就可以说是当时候世界最厉害的成就了,而我们所读的历史,或者是接受到的教育也是以此为傲。认为中国人果然很厉害,比起什么西方世界早了很多年得到了那么准确的π。话说,这确实是一个了不起的成就,但是只要你仔细推敲的话,你就会发现到为什么世界上其他的国家对于中国所取得的这个成绩着墨不多的原因了。
 |
| 祖冲之的肖像 图片来源:由三猎 - 自己的作品,CC BY-SA 4.0,https://commons.wikimedia.org/w/index.php?curid=54922069 |
这原因是因为,这个计算方式。不管是刘徽也好,还是祖冲之也好,他们使用的都是割圆法。所谓的割圆法,是刘徽发明出来的,简单的讲解这个方法就是在圆的内部切割正多边形出来,先割一个正六边形,然后通过面积的计算让它逼近圆的面积。再然后就切割正十二边形,算面积,再切割正二十四边形,再算面积。以此类推下去,这个切割的多边形边长越多,就越接近圆的面积,也就因此可以得到越准确的π这个数值。刘徽割出了96边形,并且用特殊的方法得到了和1536边形一样的精确度,所以得到了3.1416这个数字。而祖冲之则是在这个割圆术的基础上继续进一步切割,切到了24576边形,得出了3.1415926的数字。
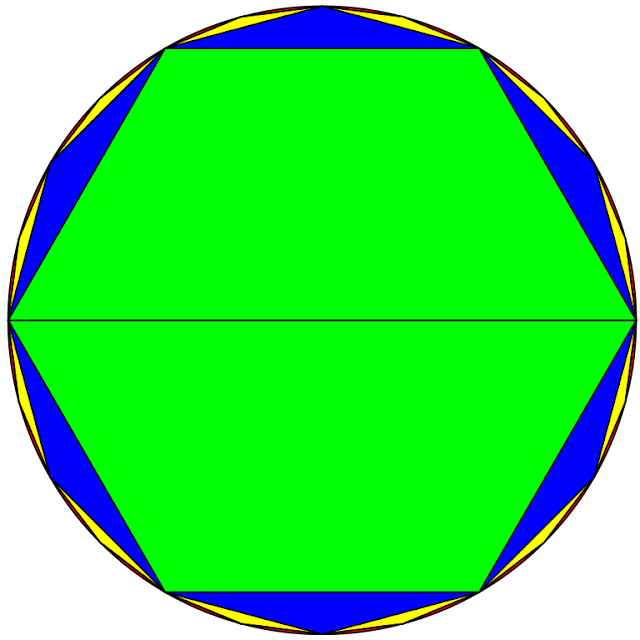 |
| 割圆法示意图 图片来源:由derivative work: Pbroks13 (talk)Cutcircle2.jpg: Gisling - Cutcircle2.jpg,CC BY-SA 3.0,https://commons.wikimedia.org/w/index.php?curid=4322998 |
在你听完了这一个方法之后,有没有发现到,其实本质上和阿基米德的方法没有差太多。虽然阿基米德的方法不够精确,计算也比较麻烦而且比较慢。但是刘徽的割圆法却可以比较容易的得到更精确的数字。所以,普遍上世界对于中国在π的成就上面的认可,其实还是归类在阿基米德这个时代的方法,并没有取得突破性的进展,或者说,没有造成了典范转移。
真正的典范转移,发生在印度。不过呢,不是因为有什么人发明了新的π的计算方法,而是发明了0到9这十个符号,也就是我们熟悉的阿拉伯数字,以及十进制。不止如此,这里还有另一个突破性的进展,那就是要归功于波斯人发明的代数,也就是假设一个未知数,然后通过等量公理移项的办法来计算这个未知数这种办法。结合了代数、阿拉伯数字以及十进制,才真正的让之前的那些多边形的计算工作取得了重大的突破。因为不管是周长的计算还是面积的计算,这些计算工作可以变得简单,是必须要用到代数、阿拉伯数字、和十进制的方法的。
基于这些突破,法国数学家,Francois Viete,用393,216边形计算π。然后,一位荷兰数学家,Ludolph van Ceulen花了25年的时间,用了一个拥有2的62次方的多边形,这是4,611,686,018,427,387,904边形。单单念就快没力了,更不用说去计算这个多边形所包夹的圆的周长或者是面积。而这个数量的多边形,得到了35个π的正确的小数位。而有趣的是,这些数字被刻在了这位大神的墓碑上面。
 |
| 花了一生人计算π的大神,Ludolph van Ceulen的墓碑 图片来源:https://www.joyofpi.com/pifacts4.html |
故事发展到这里的时候,我们似乎看到了尽头,因为再往下,就是看谁有本事可以将这个多边形的边长增加,然后因此会增加出一堆可怕以及冗长的计算,然后得到π的更加准确近似值。但是,故事并没有在这里结束,相反,π的计算再次迎来了突破,再次经历一次典范转移,那就是用无限数列来计算π。而第一个使用无限数列来计算π的人,应该是牛顿。或者说,第一个真正把无限数列发扬光大的人,是牛顿。
为什么要说这一个补充呢?原因是因为,如果你查数学历史的话,你会发现到,第一个对π这个数字进行无限数列的人,是一个印度数学家,Madhava of Sangamagrama。他是第一个提出了这样的一个数列来进行π的运算的。
 |
| Leibniz formula for π 图片来源:https://en.wikipedia.org/wiki/Leibniz_formula_for_%CF%80 |
可惜的是,这个计算流程和证明过程并没有留下来,而后人的证明,却必须要用到牛顿所发明的微积分。因此,我们不知道为什么这位印度数学家可以得到这么漂亮的无限数列来计算π。
讲到这里,就要回到这位我们大家都知道他是怎么做的牛顿,也是因为牛顿用了无限数列的办法,才让π这个数字的计算,进行了再一次的典范转移。那么牛顿的推导过程又是怎样的呢?我们明天继续聊。
最后要问大家的问题就是,在工程学的角度来看,π的近似值有个四到五个小数位就足够精确了,那么为什么还有那么多的人前扑后续的计算出π后面的小数位出来呢?你觉得π这个无理数的小数位计算,有什么意义?欢迎在下方的留言区留言,和我分享讨论吧。
今天就讲到这里,如果你喜欢这一集的内容,就请你按赞并且分享给你的朋友。如果你认为我所制作的内容对你有所帮助的话,就请你不要吝啬于订阅我的频道,同时别忘了开启小铃铛,那么你就不会错过接下来的资讯了。天地海课室,陪你每天进步1%。我们明天见。
天地海 著
没有评论:
发表评论